Probabilities

Probabilities

Probability distributions are useful to answer a myriad of questions. The python packages of numpy and scipy offer a number of probability distributions to answer questions on the likelihood of an event or describing all the likely values of a random variable.

Normal Distribution

A normal distribution also known as a Gaussian is a fairly common probability distribution that can help to answer many different types of questions. Let's work with a problem around

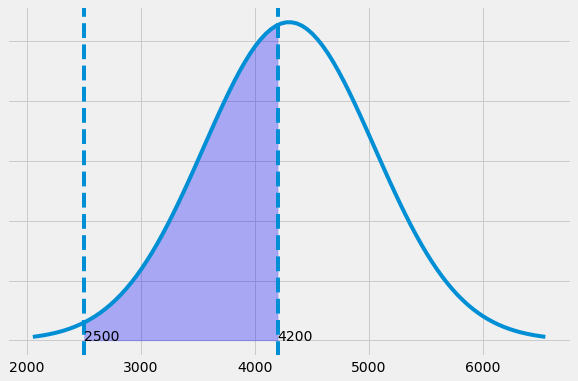
On average 4,300 acres burn per year in the state of Matto Grosso Brasil, with a standard deviation of 750 acres. The distribution of the number of acres burned follows a normal distribution. What is the probability that between 2,500 and 4,200 acres will be burned in any given year?

μ=4300

σ=750

P(2500<X<4200)=P(−2.40<Z<−0.13)

P(−2.40<Z<−0.13)=P(Z<−0.13)−P(Z<−2.40)

P(−2.40<Z<−0.13)=0.4483−0.0082=0.4401

def probability(x1,x2,mu,sigma):
        prob1 = st.norm.cdf((x1-mu)/sigma)
    prob2 = st.norm.cdf((x2-mu)/sigma)
    x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
    plt.style.use('fivethirtyeight')
    fig, ax = plt.subplots(figsize=(9,6))
    ax.set_yticklabels([])
    plt.axvline(x=x1,ls='--')
    plt.text(x1,0,'{0}'.format(x1),rotation=0)
    plt.axvline(x=x2,ls='--')
    plt.text(x2,0,'{0}'.format(x2),rotation=0)
    ax.fill_between(x_2,y,0, alpha=0.3, color='b')
    ax.plot(x, st.norm.pdf(x, mu, sigma))
    return prob2 - prob1

probability(2500,4200,4300,750)

P≈.44

Poisson Distribution

This probability distribution is used when the outcome of an experiment is a random variable,x

Vehicles pass through a junction on a busy road at an average rate of 300 per hour.

1. Find the probability that none passes in a given minute.
2. What is the expected number passing in two minutes?
3. Find the probability that this expected number actually pass through in a given two-minute period.

References:

https://en.wikipedia.org/wiki/List_of_probability_distributions