Particle Swarm Optimization

Using Particle Swarm Optimization

Particle Swarm Optimization introduces momentum to acceralte converge toward minima. Each individual, or particle, in the population keeps track of its current position, velocity, and best position it has seen so far. Momentum allows an individual to accumulate speed in a favorable direction independent of local perturbations.

Testing using Ackley Function

$$f(x)=-a\exp(-b\sqrt(\frac{1}{d}\sum_i^dx_i^2)-\exp(\frac{1}{d}\sum_i^d\cos(cx_i))+a+\exp(1)$$

$$a = 20, b = 0.2,c=2\pi$$

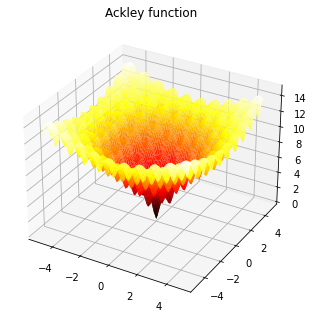
The Ackley function is widely used for testing optimization algorithms. In its two-dimensional form, as shown in the plot above, it is characterized by a nearly flat outer region, and a large hole at the centre. The function poses a risk for optimization algorithms, particularly hillclimbing algorithms, to be trapped in one of its many local minima.

Visualize Ackley Function

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def draw_pic(X, Y, Z, z_max, title, z_min=0):
    fig = plt.figure()
    ax = Axes3D(fig)
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.hot)
    ax.set_zlim(z_min, z_max)
    ax.set_title(title)
    plt.show()

def Ackley(X_min = -5, X_max = 5, Y_min = -5, Y_max = 5):
    X = np.arange(X_min, X_max, 0.1)
    Y = np.arange(Y_min, Y_max, 0.1)
    X, Y = np.meshgrid(X, Y)
    Z = -20 * np.exp(-0.2 * np.sqrt(0.5 * (X**2 + Y**2))) - \
        np.exp(0.5 * (np.cos(2 * np.pi * X) + np.cos(2 * np.pi * Y))) + np.e + 20
    return X, Y, Z, 15, "Ackley function"

PSO Algorithm

Import these following python packages.

from __future__ 
import division
import random
import math

Let's begin by building a class object for the Particle.

class Particle:
    def __init__(self,x0):
        self.position_i=[]          # particle position
        self.velocity_i=[]          # particle velocity
        self.pos_best_i=[]          # best position individual
        self.err_best_i=-1          # best error individual
        self.err_i=-1               # error individual

References:

https://www.sfu.ca/~ssurjano/ackley.html