Outlier Detection

What is an Outlier?

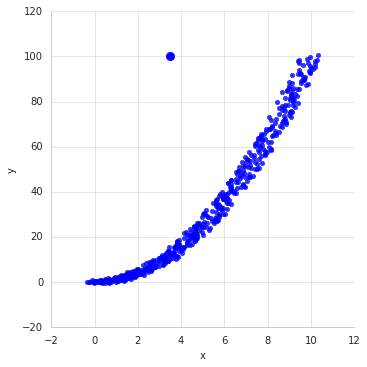
An outlier is a data point that is considered not representative from the rest of the data or if it causes problems in a standard statistical procedure. Outliers are actually fairly common within certain generating processes. Any observation featuring an abnormal distance from other values within the sample population is considered an outlier. A visual example of an outlier can be seen in the following plot. The datum at the coordinates (3.5,100) is clearly the outlier within this data set. Visual inspection is used often to see extreme values but as you increase dimensionality you will need much more clever ways to detect outliers.

Why do we care?

Outliers tend to negatively impact your model's robustness. Now sometimes we may actually want to detect outliers like for example anomalous web traffic (hacking activity), fradulent credit card transactions, event detection, and many more use cases. Now, you may also want to maintain outliers because that is all the data you have and it is naturally occurring such as predicting 1000 year flood events. So, you need to ask yourself why certain data should stay within data.

Usage of Outlier Detection

Outlier detection is useful allowing a researcher to identify and then remove data that deviates so significantly from data generating process that it affects the robustness of a model.

How are Outliers Generated?

• Data entry errors (human errors) i.e fat finger in data entry
• Mismeasurement (instrument errors) i.e instruments not calibrated
• Experimental errors (data extraction or experiment planning/executing errors)
• Intentional (dummy outliers made to test detection methods) i.e creating a male exogenous variable
• Data processing errors (data manipulation or data set unintended mutations)
• Sampling errors (extracting or mixing data from wrong or various sources)
• Natural (not an error, novelties in data)

Types of Outliers

Univariate

Multivariate

Visual Outlier Inspection

Outlier Identification Solutions

• Z-Score or Extreme Value Analysis (parametric)
• Probabilistic and Statistical Modeling (parametric)
• Linear Regression Models (PCA, LMS)
• Proximity Based Models (non-parametric)
• Information Theory Models
• High Dimensional Outlier Detection Methods (high dimensional sparse data)

Automatic Outlier Detection

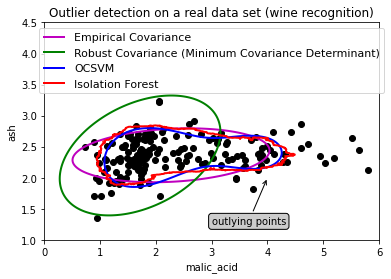
We will review scikit-learn library that offers built-in automatic methods for detecting outliers within our input data. We will use the wine data from preloaded datasets from scikit-learn looking at malaic acid

Isolation Forest

• Isolation Forest is an outlier detection technique that identifies anomalies instead of normal observations
• Similarly to Random Forest, it is built on an ensemble of binary (isolation) trees
• It can be scaled up to handle large, high-dimensional datasets

Minimum Covariance Determinant

Local Outlier Factor

One-Class SVM

Code

import numpy as np
from sklearn.covariance import EllipticEnvelope
from sklearn.svm import OneClassSVM
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn.ensemble import IsolationForest
from sklearn.datasets import load_wine

# Define "classifiers" to be used
classifiers = {
    "Empirical Covariance": EllipticEnvelope(support_fraction=1.,
                                             contamination=0.25),
    "Robust Covariance (Minimum Covariance Determinant)":
    EllipticEnvelope(contamination=0.25),
    "OCSVM": OneClassSVM(nu=0.25, gamma=0.35),
    "Isolation Forest":IsolationForest()}
colors = ['m', 'g', 'b','r']
legend1 = {}
legend2 = {}

# Get data
X1 = load_wine()['data'][:, [1, 2]]  # two clusters

# Learn a frontier for outlier detection with several classifiers
xx1, yy1 = np.meshgrid(np.linspace(0, 6, 500), np.linspace(1, 4.5, 500))
for i, (clf_name, clf) in enumerate(classifiers.items()):
    plt.figure(1)
    clf.fit(X1)
    Z1 = clf.decision_function(np.c_[xx1.ravel(), yy1.ravel()])
    Z1 = Z1.reshape(xx1.shape)
    legend1[clf_name] = plt.contour(
        xx1, yy1, Z1, levels=[0], linewidths=2, colors=colors[i])

legend1_values_list = list(legend1.values())
legend1_keys_list = list(legend1.keys())

# Plot the results (= shape of the data points cloud)
plt.figure(1)  # two clusters
plt.title("Outlier detection on a real data set (wine recognition)")
plt.scatter(X1[:, 0], X1[:, 1], color='black')
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
plt.annotate("outlying points", xy=(4, 2),
             xycoords="data", textcoords="data",
             xytext=(3, 1.25), bbox=bbox_args, arrowprops=arrow_args)
plt.xlim((xx1.min(), xx1.max()))
plt.ylim((yy1.min(), yy1.max()))
plt.legend((legend1_values_list[0].collections[0],
            legend1_values_list[1].collections[0],
            legend1_values_list[2].collections[0],
            legend1_values_list[3].collections[0]),
           (legend1_keys_list[0], legend1_keys_list[1], legend1_keys_list[2],legend1_keys_list[3]),
           loc="upper center",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.ylabel("ash")
plt.xlabel("malic_acid")

plt.show()

References:

https://www.kdnuggets.com/2017/01/3-methods-deal-outliers.html

https://scikit-learn.org/stable/modules/outlier_detection.html

https://archive.siam.org/meetings/sdm10/tutorial3.pdf

https://ieeexplore.ieee.org/abstract/document/4781136

https://towardsdatascience.com/a-brief-overview-of-outlier-detection-techniques-1e0b2c19e561